[Kaggle] sklearn Linear Regression function

LinearRegression(*, fit_intercept=True, copy_X=True, n_jobs=None, positive=False)

model.score() -> 회귀모델의 성능지표인 R^2(R-squared) score, 결정계수입니다. 상관계수를 제곱한 값으로 보면 되며 변수간 영향을 주는 정도 또는 인과관계를 정량화해서 나타낸 것입니다. 

사이킷런의 회귀 모델 클래스들은 RegressorMixin 클래스를 상속합니다. 결정 계수 Coefficient of determination는 -1~1 사이의 값을 가지며 공식은 다음과 같습니다.

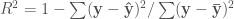
여기에서 y바는 타깃 데이터의 평균입니다. 이 공식을 직접 쓰면 다음과 같습니다

y_pred = lr.predict(X_test)
r2 = 1 - ((y_test - y_pred)**2).sum() / ((y_test - y_test.mean())**2).sum()
print(r2)

LinearRegression 클래스가 구한 모델 파라미터는 가중치와 절편이 coef_와 intercept_ 인스턴스 변수에 따로 저장되어 있습니다. 하나의 특성만 사용했기 때문에 구해진 가중치 배열의 원소가 하나입니다.

print(lr.coef_, lr.intercept_)

[0.41788087] 0.44967564199686194

 

 

Ordinary least squares Linear Regression.

LinearRegression fits a linear model with coefficients w = (w1, ..., wp) to minimize the residual sum of squares between the observed targets in the dataset, and the targets predicted by the linear approximation.

Parameters

• fit_intercept: bool, default=True Whether to calculate the intercept for this model. If set to False, no intercept will be used in calculations (i.e. data is expected to be centered). -> 모형에 상수항이 있는가. 상수항 없으면 0으로.
• copy_X: bool, default=True If True, X will be copied; else, it may be overwritten.
• n_jobs: int, default=None The number of jobs to use for the computation. This will only provide speedup in case of sufficiently large problems, that is if firstly n_targets > 1 and secondly X is sparse or if positive is set to True. None means 1 unless in a joblib.parallel_backend context. -1 means using all processors. See Glossary <n_jobs> for more details. -> 빠르게 만들 때
• positive: bool, default=False When set to True, forces the coefficients to be positive. This option is only supported for dense arrays.
• Added in 0.24

Attributes

• coef_: array of shape (n_features, ) or (n_targets, n_features) Estimated coefficients for the linear regression problem. If multiple targets are passed during the fit (y 2D), this is a 2D array of shape (n_targets, n_features), while if only one target is passed, this is a 1D array of length n_features.
• rank_: int Rank of matrix X. Only available when X is dense.
• singular_: array of shape (min(X, y),) Singular values of X. Only available when X is dense.
• intercept_: float or array of shape (n_targets,) Independent term in the linear model. Set to 0.0 if fit_intercept = False.
• n_features_in_: int Number of features seen during fit.
• Added in 0.24
• feature_names_in_: ndarray of shape (n_features_in_,) Names of features seen during fit. Defined only when X has feature names that are all strings.
• Added in 1.0

See Also

• Ridge: Ridge regression addresses some of the problems of Ordinary Least Squares by imposing a penalty on the size of the coefficients with l2 regularization.
• Lasso: The Lasso is a linear model that estimates sparse coefficients with l1 regularization.
• ElasticNet: Elastic-Net is a linear regression model trained with both l1 and l2 -norm regularization of the coefficients.

Notes

From the implementation point of view, this is just plain Ordinary Least Squares (scipy.linalg.lstsq) or Non Negative Least Squares (scipy.optimize.nnls) wrapped as a predictor object.

Examples

import numpy as np
from sklearn.linear_model import LinearRegression
X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
# y = 1 * x_0 + 2 * x_1 + 3
y = np.dot(X, np.array([1, 2])) + 3
reg = LinearRegression().fit(X, y)
reg.score(X, y)
1.0
reg.coef_
array([1., 2.])
reg.intercept_
3.0...
reg.predict(np.array([[3, 5]]))
array([16.])

 

 

추후 목록링크정리

from sklearn.linear_model import LinearRegression